Найти sin 2a может показаться сложной задачей для тех, кто только начинает изучать математику. Однако, это одно из базовых умений и знаний в тригонометрии, которое часто используется в вычислительных задачах и в научных исследованиях.
В этой статье мы рассмотрим простое объяснение того, что такое sin 2a, как его найти и какие есть способы его использования в жизни. Для лучшего понимания мы представим примеры, которые помогут вам лучше усвоить материал.
Готовы начать? Давайте разберемся с sin 2a по шагам и сделаем ваше изучение тригонометрии более простым и интересным!
Как найти sin 2a: полный гайд
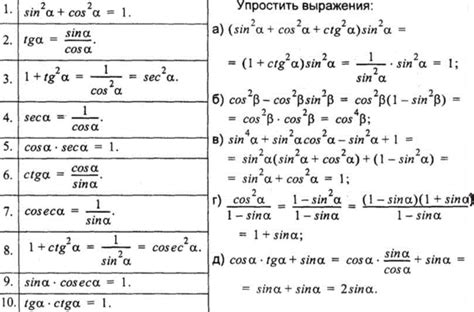
Что такое sin 2a?
sin 2a – это тригонометрическая функция, которая выражается через синус удвоенного угла a. В математике sin 2a используется во многих формулах и уравнениях.
Как найти sin 2a?
Существует несколько способов для вычисления sin 2a:
- Используя формулу sin 2a = 2sin a*cos a
- Используя формулу sin 2a = sin(a+a)
- Используя таблицу значений тригонометрических функций
Пример вычисления sin 2a
Пусть дан угол a = 30 градусов. Тогда:
- sin 2a = 2sin a*cos a = 2sin 30*cos 30 = 0,5*√3/2 = √3/4
- sin 2a = sin(a+a) = sin 60 = √3/2
Заключение
Вычисление sin 2a может показаться сложным на первый взгляд, но при использовании соответствующих формул и таблиц значений тригонометрических функций, задача становится проще. Важно не путать формулы и правильно подставлять значения, чтобы получить верный результат.
Что такое sin 2a и для чего он нужен

sin 2a - это тригонометрическая функция, которая используется в математике и физике. Она представляет собой синус двойного угла "а".
Для чего нужно знать значение sin 2a? Эта функция находит широкое применение во многих областях науки и техники. Например, в математике ее используют для решения уравнений, в физике - для описания колебаний и волн, в геодезии - для определения расстояний и высот, в машиностроении - для расчета напряжений и деформаций.
Кроме того, значение sin 2a может помочь в проведении простых геометрических выкладок, в построении графиков функций и в программировании.
Простое объяснение способов нахождения sin 2a
Первый способ
Угол 2a можно представить в виде суммы двух одинаковых углов: 2a = a + a. Имея формулу sin (a + b) = sin a * cos b + cos a * sin b, мы можем заменить a на (a + a) и b на (-a), тогда получим:
- sin (a + a) = sin a * cos a + cos a * sin a = 2 * sin a * cos a
- sin 2a = 2 * sin a * cos a
Таким образом, мы можем найти sin 2a, если знаем значения синуса и косинуса угла a.
Второй способ
Существует формула dvojak для нахождения sin 2a:
- sin 2a = 2 * sin a * cos a
Где sin a - это значение синуса угла a, а cos a - это значение косинуса угла a.
Эту формулу можно вывести, используя формулу sin (a + b) = sin a * cos b + cos a * sin b:
- sin (a + a) = sin a * cos a + cos a * sin a
- 2 * sin a * cos a = sin (a + a)
- sin 2a = 2 * sin a * cos a
Третий способ
Можно использовать формулу Эйлера:
- e^(ix) = cos x + i * sin x
Где i - это мнимая единица, a x - это любой угол в радианах. Возведя в квадрат обе части формулы, получим:
- e^(2ix) = cos 2x + i * sin 2x
Таким образом, у нас есть:
- cos 2x = Re(e^(2ix))
- sin 2x = Im(e^(2ix))
Это позволяет найти значение sin 2a, зная значение угла a в радианах.
Примеры решения задач на нахождение sin 2a

Пример 1
Найти sin 2a, если a = 30°.
Решение:
- sin 2a = 2sin a cos a
- sin 30° = 1/2
- cos 30° = √3/2 (значение можно найти в таблице значений функций)
- sin 2a = 2(1/2)(√3/2) = √3
Ответ: sin 2a = √3
Пример 2
Найти sin 2a, если a = π/6.
Решение:
- sin 2a = 2sin a cos a
- sin(π/6) = 1/2
- cos(π/6) = √3/2 (значение можно найти в таблице значений функций)
- sin 2a = 2(1/2)(√3/2) = √3
Ответ: sin 2a = √3
Пример 3
Найти sin 2a, если a = 45°.
Решение:
- sin 2a = 2sin a cos a
- sin 45° = √2/2
- cos 45° = √2/2 (значение можно найти в таблице значений функций)
- sin 2a = 2(√2/2)(√2/2) = 1
Ответ: sin 2a = 1
Пример 4
Найти sin 2a, если a = 60°.
Решение:
- sin 2a = 2sin a cos a
- sin 60° = √3/2
- cos 60° = 1/2 (значение можно найти в таблице значений функций)
- sin 2a = 2(√3/2)(1/2) = √3
Ответ: sin 2a = √3
Вопрос-ответ

Как найти sin 2a?
Для нахождения sin 2a можно использовать тригонометрические формулы: sin 2a = 2sin a cos a или sin 2a = (2tan a) / (1 + tan^2 a).
Что такое sin 2a?
sin 2a - это тригонометрическая функция, которая возвращает значение синуса угла, равного удвоенному углу a. Формула sin 2a = 2sin a cos a является частным случаем более общей формулы для нахождения sin (n * a), где n - любое целое число.
Какую роль играют формулы в нахождении sin 2a?
Формулы для нахождения sin 2a позволяют упростить вычисления и сократить количество операций, необходимых для получения результата. Без использования формул расчеты могут быть громоздкими и трудоемкими.
Как использовать формулы для нахождения sin 2a в практических задачах?
Формулы для нахождения sin 2a могут быть использованы, например, в задачах геометрии, физики, астрономии и других науках. Например, для нахождения площади треугольника, заданного двумя сторонами и углом между ними, можно использовать формулу S = (1/2) a b sin C, где C - угол между сторонами, который можно выразить через sin 2a с помощью формулы sin C = 2sin a cos a.
Как проверить правильность вычисления sin 2a?
Если вы не уверены в правильности вычислений, можно проверить результат с помощью обратных тригонометрических функций. Например, для проверки sin 2a можно использовать функцию arcsin, вычислив arcsin (sin 2a) и сравнив результат с удвоенным углом a. Если они равны, то вычисления верны.
Как находить sin 2a без использования тригонометрических формул?
Без использования формул нахождение sin 2a может быть достаточно сложным и требовательным к вычислительным ресурсам. Однако можно использовать графики функций, таблицы значений или другие методы для приближенного вычисления значения sin 2a. Например, с помощью табличных значений или калькулятора можно найти значение sin a, а затем применить формулу sin 2a = 2sin a cos a.