Одной из основных задач в геометрии является определение площади фигур. При этом иногда нужно найти не только площадь, но и некоторые другие характеристики фигуры. Например, в случае трапеции может понадобиться найти синус угла между ее боковыми сторонами. В этой статье мы рассмотрим, как найти sin трапеции, приведем формулы и примеры расчета.
Трапеция - это фигура, которая имеет две параллельные стороны и две непараллельные. Для трапеции можно выделить два основания - параллельные стороны. Длина каждого из оснований обозначается соответственно a и b. Высота h трапеции - это расстояние между основаниями, она перпендикулярна к обоим основаниям. Точка пересечения высоты с боковой стороной трапеции называется основанием высоты.
Если в трапеции известны основания и высота, то ее площадь может быть вычислена по формуле S=(a + b) * h / 2. Однако иногда нужно найти и синус угла α между боковыми сторонами (α обычно обозначается как угол A или угол B, в зависимости от того, какая из сторон соответствующего основания). Для этого требуется применить теорему синусов.
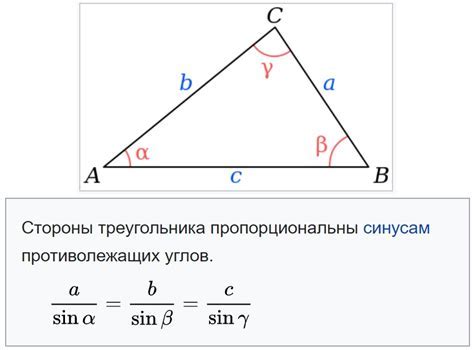
Теорема синусов утверждает, что для произвольного треугольника со сторонами a, b и c, противолежащими углам α, β и γ соответственно, верно равенство sin α / a = sin β / b = sin γ / c.
Таким образом, если мы знаем длину боковой стороны трапеции и угол между этой стороной и основанием, то можем найти значение синуса этого угла. В этом случае опять же используется теорема синусов, но уже для треугольника, который образуется высотой и боковой стороной трапеции.
Понимание синуса трапеции
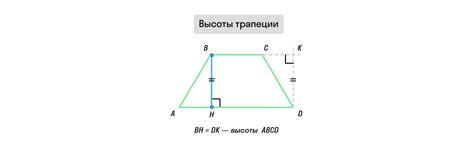
Трапеция - это фигура, имеющая две параллельные стороны, называемые основаниями, и две боковые стороны, называемые боковыми сторонами. Средняя линия трапеции - это средняя линия, соединяющая середины оснований.
Синус трапеции - это отношение высоты трапеции к её длине.
Чтобы найти синус трапеции, нужно знать высоту и длину трапеции. Если высота и длина сторон известны, синус трапеции можно вычислить по формуле:
sin(α) = h / (b1 - b2)
где α - угол между боковой стороной и одним из оснований, h - высота трапеции, b1 и b2 - длины оснований.
Если же синус трапеции необходимо найти по значениям угла α и длин оснований, то формула будет выглядеть следующим образом:
sin(α) = 2 * h / (b1 + b2)
где α - угол между боковой стороной и одним из оснований, h - высота трапеции, b1 и b2 - длины оснований.
Найденное значение синуса трапеции может быть использовано, например, для расчета площади трапеции или для нахождения других параметров фигуры.
Формула для расчета
Формула для нахождения sin трапеции
Для расчета sin трапеции необходимо знать ее высоту h и угол при большем основании α. Используется формула:
sin α = h / (a + b) * 2
где:
- α - угол при большем основании, градусы
- h - высота трапеции, единицы измерения соответствуют единицам измерения оснований
- a и b - длины оснований трапеции, единицы измерения соответствуют единицам измерения высоты
Пример расчета
Рассмотрим пример: у трапеции основания равны a = 5 см и b = 10 см, а высота h = 4 см. Найдем sin угла при большем основании:
| a | b | h | |
|---|---|---|---|
| Значение: | 5 см | 10 см | 4 см |
sin α = h / (a + b) * 2 = 4 / (5 + 10) * 2 ≈ 0,364
Таким образом, sin угла при большем основании трапеции с высотой 4 см и основаниями 5 см и 10 см примерно равен 0,364.
Примеры расчета sin трапеции
Пример 1
Дана трапеция ABCD, где AB=5 см, CD=8 см, BC=6 см и AD=7 см. Найдем значение sin угла ABD.
| Сторона | Длина |
|---|---|
| AB | 5 см |
| CD | 8 см |
| BC | 6 см |
| AD | 7 см |
Для нахождения sin угла ABD воспользуемся формулой sin(ABD) = (AD-BC)/AB = (7-6)/5 = 0.2.
Пример 2
Дана трапеция ABCD, где AD=5 см, BC=10 см, AB= 8 см и CD=6.5 см. Найдем значение sin угла CDA.
| Сторона | Длина |
|---|---|
| AD | 5 см |
| BC | 10 см |
| AB | 8 см |
| CD | 6.5 см |
Для нахождения sin угла CDA воспользуемся формулой sin(CDA) = (BC-AD)/CD = (10-5)/6.5 = 0.77.
Выводы и рекомендации

1. Важность знания формулы для расчета
Для корректного вычисления sin трапеции необходимо знать соответствующую формулу. Важно понимать, что при наличии неправильной формулы можно получить неверный результат. Поэтому перед расчетами следует убедиться в правильности применяемой формулы.
2. Пример использования формулы
Рассмотрим пример расчета sin трапеции. Пусть основания трапеции равны 6 и 10, а высота равна 8. Используя формулу sin(α) = (b - a) / 2h, где b и a - основания трапеции, h - высота, получаем:
| Параметр | Значение |
|---|---|
| b | 10 |
| a | 6 |
| h | 8 |
| sin(α) | 0,5 |
Таким образом, sin трапеции с основаниями 6 и 10 и высотой 8 равен 0,5.
3. Рекомендации по использованию
- Перед расчетом всегда убедитесь в правильности использования формулы.
- Используйте калькулятор для проверки расчетов.
- Учитывайте единицы измерения при вводе данных и выводе результата.
- При необходимости округляйте результат до нужного количества знаков после запятой.
Вопрос-ответ

Как определить значение sin трапеции, если известны углы?
Для нахождения sin трапеции нужно знать длины ее оснований и угол между ними. Формула выражается как (b-a) / 2h, где a и b - длины оснований, h - высота трапеции. Угол между основаниями можно найти, используя формулу sinA = h/(b-a). Таким образом, зная угол и длины оснований, можно найти sin трапеции.
Какой метод лучше всего использовать для нахождения sin трапеции?
Один из простых способов нахождения sin трапеции - использовать формулу (b-a) / 2h. Эта формула основана на теореме синусов, поэтому не требует специальных знаний. Однако, если у вас есть данные о боковых сторонах трапеции, можно использовать более сложную формулу, которая также учитывает их длины.
Как можно найти sin трапеции, если не известны углы, но есть данные о диагоналях?
Если известны диагонали трапеции, можно использовать формулу sinA = 2S/ab, где S - площадь трапеции, a и b - диагонали трапеции. Чтобы найти площадь трапеции, нужно использовать формулу S = (a+b)h/2, где h - высота трапеции.
Как можно использовать sin трапеции в геометрических расчетах?
Sin трапеции можно использовать для определения угловой величины. Например, если известен угол между основаниями трапеции, можно использовать формулу sinA = h/(b-a), чтобы найти sin угла. Затем, используя формулу sinA = opp/hyp, можно найти размер угла. Эти расчеты могут быть полезны при решении задач на геометрию и механику.
Что такое трапеция и как она отличается от параллелограмма?
Трапеция - это фигура, которая имеет два параллельных основания и две непараллельные боковые стороны. Она отличается от параллелограмма тем, что у параллелограмма все четыре стороны параллельны. Также, в трапеции углы при основаниях не обязательно равны, в отличие от параллелограмма.
Можно ли использовать sin трапеции для определения гипотенузы треугольника?
Нет, sin трапеции не может быть использован для нахождения гипотенузы треугольника, так как трапеция имеет только две параллельные стороны. Для определения гипотенузы треугольника нужно использовать теорему Пифагора или другие методы вычисления треугольников.