В тригонометрии, тангенс - это отношение противоположной стороны к ближайшей катете в прямоугольном треугольнике. Расчеты тангенса могут быть сложными, особенно если данный элемент отсутствует в таблице тригонометрических значений. Однако существует простой способ расчета тангенса, если известен синус угла.
Перед расчетом тангенса, необходимо помнить, что синус и тангенс связаны следующим образом: тангенс угла равен отношению синуса угла к косинусу угла. Другими словами,
tg(a) = sin(a) / cos(a)
В прямоугольном треугольнике, косинус угла можно рассчитать как отношение прилежащей стороны к гипотенузе. Если известен синус угла, то воспользовавшись формулой Пифагора, можно рассчитать катет противоположный углу, а затем посчитать косинус и тангенс.
Как найти тангенс синуса: простой способ расчета

Тангенс синуса - это отношение синуса угла к косинусу угла. То есть, tg(sin) = sin / cos.
Допустим, нам известен синус угла. Чтобы найти тангенс, нам нужно также знать косинус угла. Как его найти? Просто воспользуемся тождеством sin² + cos² = 1. Тогда cos = sqrt(1 - sin²).
Теперь мы можем легко посчитать tg(sin). Пример:
- Дано: sin = 0.6.
- cos = sqrt(1 - 0.6²) = 0.8.
- tg(sin) = 0.6 / 0.8 = 0.75.
Простой способ расчета тангенса синуса позволяет нам быстро получить ответ без необходимости поиска значений в таблицах или использования сложных формул. Попробуйте использовать этот метод при решении задач на нахождение тангенса синуса.
Основные понятия тригонометрии
Тригонометрия - это наука о пропорциях между сторонами и углами в треугольниках. Ключевыми понятиями тригонометрии являются синус, косинус и тангенс. Эти функции выражают отношения между различными сторонами треугольника и могут быть использованы для решения многих задач.
Синус - это отношение противоположной стороны к гипотенузе в треугольнике. Косинус - это отношение прилегающей стороны к гипотенузе, а тангенс - это отношение противоположной стороны к прилегающей.
Тригонометрические функции могут быть выражены как в градусах, так и в радианах. Градусы - это мера угла, выраженная в градусах, а радианы - это мера угла, выраженная в единицах длины.
Тригонометрические функции широко используются в математике, физике, инженерии и других науках. Они позволяют решать многие задачи, связанные с треугольниками и углами.
Для удобства вычислений тригонометрические значения обычно табулируются в таблицах, а также могут быть вычислены с помощью специальных калькуляторов и компьютерных программ.
- Примеры использования тригонометрических функций:
- определение высоты или длины недостающей стороны треугольника;
- вычисление расстояний между космическими объектами;
- построение трехмерной графики;
- расчет угловых скоростей и ускорений;
- определение точек на земной поверхности по географическим координатам.
Основные понятия тригонометрии необходимы для понимания более высоких математических концепций и широко используются в практических приложениях.
Формула тангенса через синус
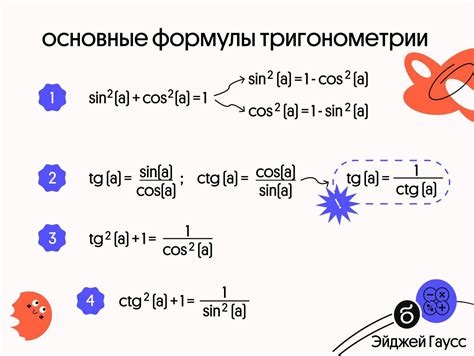
Формула тангенса связывает значения тангенса и синуса для заданного угла:
| tg θ = sin θ / cos θ |
При этом, зная значение синуса, можно найти значение тангенса, используя данную формулу.
Для этого нужно расчитать значение косинуса, используя формулу:
| cos θ = √(1 - sin²θ) |
После этого подставляя значения синуса и косинуса в формулу тангенса, можно получить его значение.
Расчет тангенса синуса вручную
Тангенс угла - это отношение синуса угла к косинусу угла. То есть тангенс угла равен синусу угла, разделенному на косинус угла. Если известен только синус угла, можно легко вычислить тангенс угла, используя простые математические формулы.
Формула:
- Тангенс угла = синус угла / косинус угла
Для вычисления тангенса угла, известного только синус угла, необходимо вычислить косинус угла, поскольку они являются взаимосвязанными величинами. Для этого можно использовать теорему Пифагора:
Теорема Пифагора:
- для прямоугольного треугольника со сторонами a, b и гипотенузой c, справедливо: c² = a² + b²
Косинус угла можно найти, если известны две стороны прямоугольного треугольника, в котором гипотенуза равна 1, а противолежащая катета - синусу угла. Итак, чтобы найти косинус угла, можно использовать следующую формулу:
- Косинус угла = √(1 - синус² угла)
Теперь у нас есть все, чтобы вычислить тангенс угла:
- Тангенс угла = синус угла / косинус угла
Этот простой метод расчета тангенса синуса может быть полезен при изучении тригонометрии в школе или при выполнении заданий на упражнение в математике.
Использование калькулятора для расчета тангенса синуса
Если вы знаете значение синуса угла, то с помощью калькулятора можно легко вычислить его тангенс. Для этого нужно нажать на кнопку "tan" на калькуляторе, ввести значение синуса и нажать на кнопку "равно". Результатом вычислений будет значение тангенса угла.
Калькулятор также позволяет вычислять тангенс с помощью формулы, связывающей синус и косинус угла. Для этого нужно возвести синус угла в степень -1 (обратное значение) и разделить результат на косинус угла. Например, если синус угла равен 0,5, то тангенс можно вычислить следующим образом:
- Вычисляем косинус угла. cos(угол) = √(1 - sin²(угол)) = √(1 - 0,5²) ≈ 0,866
- Вычисляем тангенс угла. tan(угол) = sin(угол) / cos(угол) = 0,5 / 0,866 ≈ 0,577
Таким образом, с помощью калькулятора можно быстро и удобно вычислить тангенс угла, если известно значение его синуса. Этот метод расчета особенно полезен при выполнении различных задач в математике, физике и других науках.
Расчет тангенса синуса в программе Excel

Программа Excel дает возможность быстро и легко рассчитать тангенс синуса заданного угла. Для этого необходимо воспользоваться функцией TAN, которая принимает на вход значение угла в радианах.
Для перевода угла из градусной меры в радианы используйте функцию RADIANS. Например, чтобы рассчитать тангенс синуса угла 60 градусов, необходимо выполнить следующие действия:
- Вычислить синус угла с помощью функции SIN: =SIN(RADIANS(60)). Результатом будет число, близкое к 0.87.
- Вычислить тангенс синуса с помощью функции TAN: =TAN(RADIANS(60)). Результатом будет число, близкое к 1.73.
Важно учитывать, что функция TAN может вернуть ошибку, если угол, переданный на вход, кратен 90 градусам. В этом случае можно использовать функцию IFERROR, чтобы вернуть любое другое значение вместо ошибки.
Таким образом, для расчета тангенса синуса в программе Excel нужно использовать функции SIN, TAN и, при необходимости, RADIANS и IFERROR. Это позволяет быстро и точно выполнить расчеты, не прибегая к сложным математическим формулам.
Примеры решения задач по нахождению тангенса синуса
Рассмотрим простой пример: известно, что sin A = 0,6. Найдём tg A.
Для начала вспомним формулу: tg A = sin A / cos A. Поскольку нам дан синус угла A, нам нужно найти косинус этого угла. Используя формулу, найдём косинус угла A: cos A = √(1 - sin² A) = √(1 - 0,6²) = 0,8.
Теперь, используя обе найденные величины, мы можем найти тангенс угла A: tg A = sin A / cos A = 0,6 / 0,8 = 0,75. Таким образом, tg A = 0,75.
Рассмотрим ещё один пример: sin B = 0,4. Найдём tg B.
Аналогично первому примеру, найдём косинус угла B: cos B = √(1 - sin² B) = √(1 - 0,4²) = 0,916. Затем найдём тангенс угла B: tg B = sin B / cos B = 0,4 / 0,916 ≈ 0,436. Таким образом, tg B ≈ 0,436.
И наконец, рассмотрим третий пример: sin C = 0,8. Найдём tg C.
Найдём косинус угла C: cos C = √(1 - sin² C) = √(1 - 0,8²) = 0,6. Затем, используя формулу, найдём тангенс угла C: tg C = sin C / cos C = 0,8 / 0,6 = 1,333. Таким образом, tg C = 1,333.
Полезные советы при расчетах тангенса синуса
При расчете тангенса синуса следует помнить, что тангенс является отношением синуса к косинусу:
tg(x) = sin(x) / cos(x)
Таким образом, для расчета тангенса синуса необходимо знать значения как синуса, так и косинуса угла.
Если известен только синус, можно использовать формулу косинуса через синус:
cos(x) = √(1 - (sin(x))^2)
Зная значение синуса, можно легко вычислить косинус и, соответственно, тангенс.
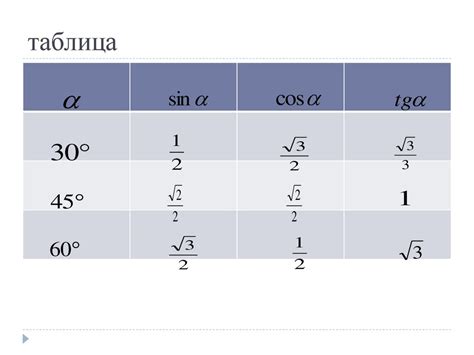
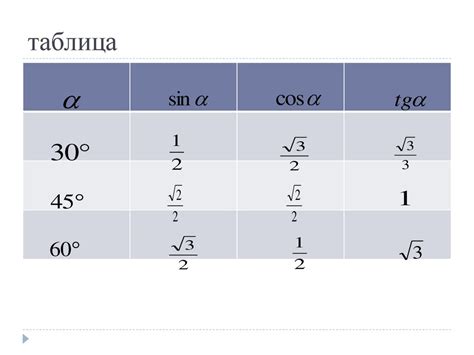
Если значения синуса и косинуса известны только для специальных углов (например, 30°, 45°, 60°), можно использовать таблицы тригонометрических функций или запомнить значения синуса, косинуса и тангенса для этих углов.
Чтобы избежать ошибок при расчетах, рекомендуется использовать калькулятор или специальные программы для вычисления тригонометрических функций.
Вопрос-ответ

Как найти тангенс, если известен синус?
Для поиска тангенса, если известен синус, можно воспользоваться формулой tg(x) = sin(x) / cos(x).
Как рассчитать косинус, если известен только синус?
Для рассчета косинуса, если известен только синус, можно воспользоваться формулой cos(x) = sqrt(1 - sin^2(x)), где x - угол в радианах.
Можно ли использовать данный способ расчета тангенса для любых углов?
Данный простой способ расчета тангенса, если известен синус, подходит только для тех углов, у которых косинус не равен нулю. Для углов близких к 90 градусам, данный способ не сработает.
В каких случаях лучше использовать другие методы расчета тангенса?
Другие методы расчета тангенса могут быть использованы для нахождения тангенса углов, близких к 90 градусам, а также для нахождения тангенса углов, выраженных в градусах. В таких случаях этот простой метод может давать неточные результаты.
Как правильно округлить результат расчета тангенса?
Округлять результат расчета тангенса необходимо до одного-двух знаков после запятой, чтобы избежать получения слишком длинных чисел, которые будут трудны для использования в дальнейших расчетах.
Какой инструмент можно использовать для расчета тангенса, если не уверен в правильности выполнения расчетов вручную?
Существует множество онлайн-калькуляторов, которые могут помочь в расчете тангенса. Также можно воспользоваться специализированными программами для математических расчетов, такими как Microsoft Excel, MathCAD или Wolfram Mathematica.