Здравствуйте, уважаемые читатели! В данной статье мы рассмотрим простой и эффективный способ нахождения третьей стороны треугольника по известным двум. Этот метод позволит вам быстро и легко решить множество задач геометрии.
Нахождение сторон треугольника по известным двум – это одна из самых часто встречающихся задач в геометрии. Это может понадобиться вам при расчетах площади и периметра треугольника, при определении углов и прочих задачах. В данной статье мы рассмотрим метод нахождения третьей стороны треугольника при условии, что известны две другие стороны и угол между ними.
Приготовьтесь к увлекательному путешествию в мир геометрии, где мы разберемся в том, как составлять формулы, как использовать тригонометрические функции и как правильно применять математические операции для решения задач.
Как найти третью сторону треугольника

Задача поиска третьей стороны
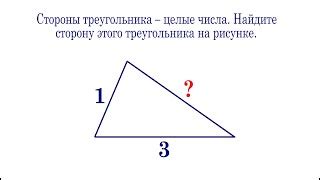
Часто возникают ситуации, когда для решения задачи нужно найти третью сторону треугольника по известным двум. Это может быть полезно при определении радиуса окружности, вписанной в треугольник, а также при рассмотрении свойств треугольников разных типов.
Формула нахождения третьей стороны треугольника
Существует легкий способ расчета длины третьей стороны треугольника по теореме Пифагора:
- Определите длины известных сторон треугольника;
- Возвести в квадрат каждую длину;
- Сложите два полученных квадрата;
- Найдите квадратный корень от суммы квадратов.
Таким образом, формула будет выглядеть как: c = √(a² + b²), где c - третья сторона треугольника, a и b - известные стороны.
Пример использования формулы
Для примера, рассмотрим треугольник со сторонами a = 3см и b = 4см.
Применяя формулу c = √(a² + b²), получим:
c = √(3² + 4²) = √(9 + 16) = √25 = 5см
Таким образом, третья сторона равна 5см.
Заключение
Нахождение третьей стороны треугольника может быть легко выполнено с помощью формулы нахождения гипотенузы треугольника по известным катетам. Однако, необходимо помнить о том, что треугольник подчиняется определенным правилам, и нахождение одной стороны может привести к возможности нахождения других параметров треугольника.
Формула для нахождения третьей стороны

Определение
Для того, чтобы найти третью сторону треугольника, необходимо знать длины двух его сторон. Данная задача решается при помощи применения теоремы Пифагора или формулы косинусов.
Применение теоремы Пифагора
Если известны длины катетов прямоугольного треугольника, то длину гипотенузы можно найти при помощи теоремы Пифагора:
c = sqrt(a^2 + b^2)
где c - длина гипотенузы, а и b - длины катетов
Применение формулы косинусов
Если треугольник не является прямоугольным, то для нахождения третьей стороны требуется использование формулы косинусов:
c^2 = a^2 + b^2 - 2ab cos(C)
где C - угол при гипотенузе c
Формула косинусов также может применяться для нахождения угла при одной из известных сторон.
Важно учитывать, что при использовании формулы косинусов углы должны быть заданы в радианах.
Примеры расчета

Пример 1
Дано: сторона АB = 5, сторона BC = 7
Найти: сторона AC
Решение:
Используем теорему Пифагора:
AC² = AB² + BC²
AC² = 5² + 7²
AC² = 25 + 49
AC² = 74
AC = √74 ≈ 8,6
Пример 2
Дано: сторона АB = 3, сторона AC = 4
Найти: сторона ВC
Решение:
Используем теорему Пифагора:
BC² = AC² - AB²
BC² = 4² - 3²
BC² = 16 - 9
BC² = 7
BC = √7 ≈ 2,65
Пример 3
Дано: сторона AB = 4, сторона BC = 5
Найти: сторона AC
Решение:
Используем теорему Пифагора:
AC² = AB² + BC²
AC² = 4² + 5²
AC² = 16 + 25
AC² = 41
AC = √41 ≈ 6,4
Всегда помните, что использование теоремы Пифагора возможно только в прямоугольном треугольнике.
Советы и рекомендации по нахождению третьей стороны треугольника
Используйте теорему Пифагора
Если известны длины двух сторон и один из углов между ними прямой, то можно использовать теорему Пифагора, чтобы найти длину третьей стороны. Согласно этой теореме квадрат длины гипотенузы (стороны, противоположной прямому углу) равен сумме квадратов длин катетов (двух сторон, прилегающих к прямому углу). Пример: если известны длины сторон a=3 и b=4, можно найти длину стороны c как c = √(a² + b²) = √(3² + 4²) = √25 = 5.
Другой способ: использование формулы косинусов
Если известны длины двух сторон и угол между ними (который не обязательно прямой), можно использовать формулу косинусов, чтобы найти длину третьей стороны. Согласно этой формуле квадрат длины третьей стороны равен сумме квадратов длин двух известных сторон минус удвоенное произведение этих сторон на косинус угла между ними. Пример: если известны длины сторон a=5 и b=8, и угол между ними равен 60 градусов, можно найти длину стороны c как c = √(a² + b² - 2ab·cos(60°)) = √(5² + 8² - 2·5·8·cos(60°)) = √(25 + 64 - 80·0.5) = √29.
Будьте внимательны при измерении сторон и углов
При измерении сторон треугольника используйте рейку или линейку, а при измерении углов - транспортир. Будьте внимательны при замере, чтобы получить точные значения. Даже маленькая погрешность при измерении может привести к неправильному результату при расчете третьей стороны.
Проверьте свой ответ
После того, как вы нашли третью сторону треугольника, проверьте свой ответ путем измерения этой стороны и сравнения с рассчитанным значением. Если результаты не совпадают, перепроверьте все изначальные данные и расчеты.
- Не забывайте проверять единицы измерения - если они не совпадают (например, одна сторона указана в сантиметрах, а другая - в метрах), необходимо перевести все значения в одну систему исчисления.
- Если известно несколько сторон и углов треугольника, можно воспользоваться законами синусов и косинусов, чтобы найти другие неизвестные значения. Имейте в виду, что эти формулы действуют только для треугольников, где стороны пропорциональны углам, и не работают для любых треугольников.
Вопрос-ответ

Как найти третью сторону треугольника, если известны длины двух других сторон?
Для этого нужно воспользоваться теоремой Пифагора: третья сторона треугольника в квадрате равна сумме квадратов двух других сторон. Например, если известны стороны a = 5 и b = 12, то третья сторона c будет равна корню из 169, то есть c = 13.
Как найти третью сторону треугольника, если известны два угла и длина одной из сторон?
Для этого нужно воспользоваться Законом косинусов: третья сторона в квадрате равна сумме квадратов двух других сторон и удвоенного произведения одной известной стороны на косинус угла между известными сторонами. Например, если известны углы A = 60 градусов, B = 40 градусов и сторона a = 8, то третья сторона c будет равна корню из 106,5, то есть c ≈ 10,318.
Как найти третью сторону треугольника, если известна длина одной стороны и два равных угла?
Если известны длина одной стороны и два равных угла, то треугольник является равнобедренным. Третья сторона будет равна длине боковой стороны, не являющейся основанием треугольника. Например, если известны углы A = 60 градусов, B = 60 градусов и сторона a = 7, то третья сторона c будет равна стороне b, которую нужно найти по формуле: b = (a * sin(A)) / sin(180 - A - B), то есть b ≈ 7.
Как найти третью сторону треугольника, если известны высота и медиана?
Если известны высота h и медиана m, то можно воспользоваться теоремой о медиане: медиана, проведенная к стороне треугольника, делит эту сторону пополам и образует два равнобедренных треугольника. Значит, длина основания одного из них будет равна половине третьей стороны, а по теореме Пифагора можно найти значение третьей стороны. Например, если известны высота h = 8 и медиана m = 10, то третья сторона c будет равна корню из 144, то есть c = 12.
Как найти третью сторону треугольника, если известны радиусы вписанной и описанной окружностей?
Для этого нужно воспользоваться формулой: третья сторона равна произведению диаметра описанной окружности на радикал из единицы, вычтенной из отношения радиусов вписанной и описанной окружностей. Например, если известны радиусы вписанной r = 3 и описанной R = 5 окружностей, то третья сторона c будет равна 2 * 5 * (1 - 3^2/5^2)^(1/2), то есть c ≈ 8.
Как найти третью сторону треугольника, если известны координаты вершин?
Если известны координаты вершин треугольника, то можно воспользоваться формулой для вычисления расстояния между двумя точками на плоскости. Например, если вершины треугольника A(0, 0), B(0, 4) и C(3, 0), то сторона AB будет равна 4, сторона BC будет равна 5, а сторона AC будет равна 3 (это можно найти по формуле: AB = ((x2 - x1)^2 + (y2 - y1)^2)^(1/2), где (x1, y1) и (x2, y2) - координаты вершин).